Расчет деревянных балок перекрытия на прочность: онлайн калькулятор

Перекрытие дома, устроенное по деревянным балкам – один из самых популярных вариантов при строительстве частных домов. Однако такой выбор требует обязательного расчета нагрузки на балку и грамотного выбора ее сечения, шага установки балок. Для упрощения этих расчетов мы предлагаем воспользоваться простым онлайн-калькулятором.

Основы вычислений

Для начала следует понять, что именно требуется рассчитать. Дело в том, что деревянный брус или доска балки под нагрузкой способно изогнуться до определенного предела – эта величина называется пределом прочности – и при дальнейшем увеличении нагрузки сломаться. Под действием нагрузки изогнувшаяся балка может также выскользнуть из креплений. Чтобы избежать этого или хотя бы снизить риск такой неприятности, деревянные балки стараются заделать в кладку дома или прикрепить с помощью кронштейнов, уголков и других видов деталей к деревянной стене дома. Используют также врубку балки в венец стены. Все такие виды фиксации считаются жесткой заделкой.

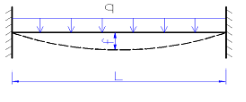
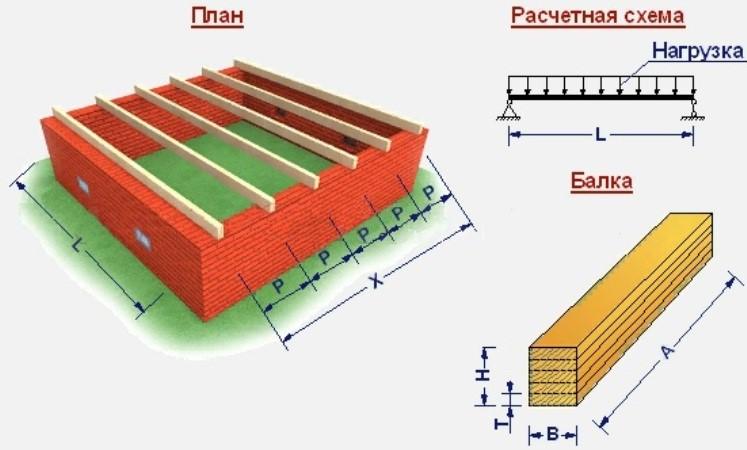
Вот так примерно выглядит расчетная схема для однопролетной балки, то есть изделие, у которого закреплены только концы. Здесь L – пролет балки, расстояние между опорными точками, Q – распределенная нагрузка, f – величина прогиба.

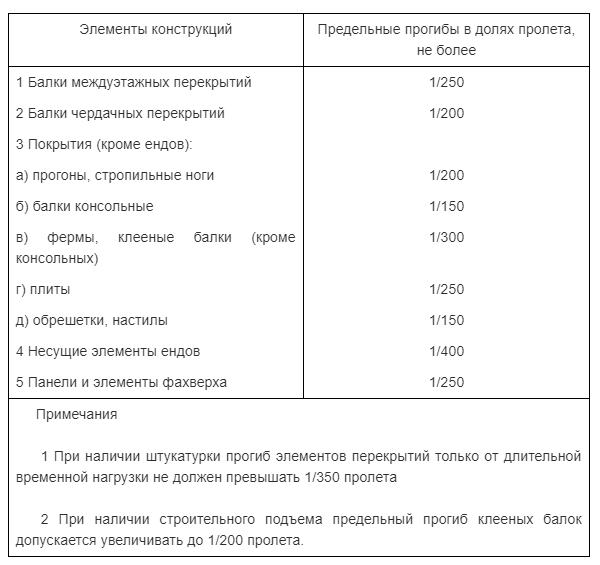
Основой для расчета предельно допустимого прогиба, как и источником других данных о работе деревянных конструкций, является СП 64.13330.2011. Согласно этому документу, предельный прогиб балки для межэтажных перекрытий не должен превышать 1/250 часть длины пролета.

То есть для балки с длиной 6 м допустимый прогиб составит 24 мм. Если же брать более строгие значения (для штукатурки на потолке и требующих строгой плоскости пола второго этажа напольных покрытий, например, плитки) – 1/350, допустимый прогиб уменьшается до 17 мм.

В целом для вычислений используют формулу f=L/350, при этом длину пролета указывают в миллиметрах.

Таблица 1.1. Допустимый прогиб деревянных конструкций.

Соответственно, при расчете балки на прочность в онлайн-калькуляторе или вручную следует уменьшать сечение только до тех пределов прогиба, которые меньше вычисленного значения.

На иллюстрации выше показана расчетная схема для распределенной нагрузки, то есть такой, которая равномерно распределяется по всей балке. Обычно в жилых помещениях используется именно эта схема. Однако при размещении в комнате мебели или оборудования большого веса, особенно не возле стены (на которую опирается край балки), а на некотором удалении от нее, иногда бывает разумнее использовать схему расчета для сосредоточенной нагрузки.

Вот так примерно создается сосредоточенная нагрузка на балку.

Таблица 1.2. Схемы расчета деревянных балок с одной сосредоточенной нагрузкой.

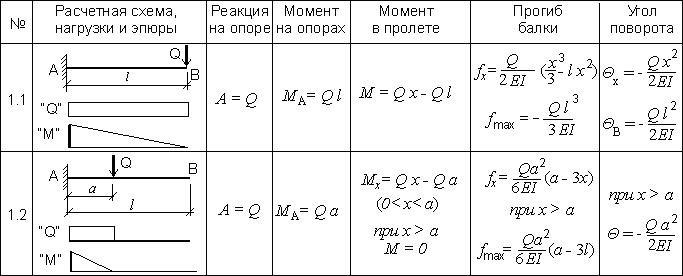
Здесь и далее Е – модуль упругости древесины Е=100 000 кгс/м2), I – осевой момент инерции балки.

Таблица 1.3. Схемы расчета деревянных балок с двумя сосредоточенными нагрузками.

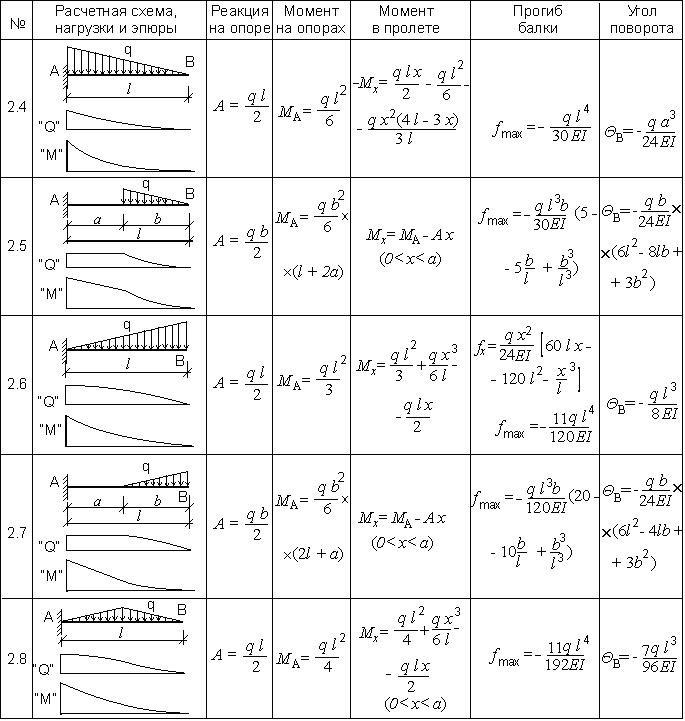
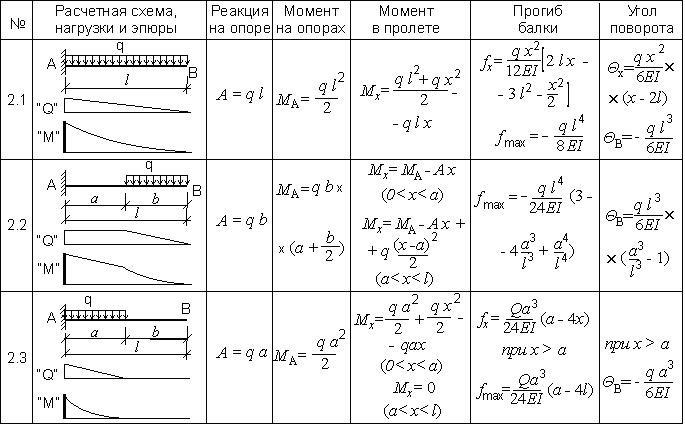
Таблица 1.4. Расчет балки с двусторонним жестким защемлением при равномерно-распределенной нагрузке.

В зависимости от того, куда именно приложены нагрузки и в каком количестве, используется расчетная схема соответствующего типа.

Для бруса, защемленного в стене только одним концом (консольное крепление), используются другие формулы расчета деревянной балки на прочность. Обычно такие вычисления нужны при проектировании навесов на деревянных балках-опорах, больших вылетов крыши и других подобных случаях.

Таблица 1.5. Расчет консольной балки при одной сосредоточенной нагрузке.

Таблица 1.6. Расчет консольной балки при одной неравномерно-распределенной нагрузке.

Таблица 1.7. Расчет консольной балки при одной равномерно-распределенной нагрузке.

Формулы кажутся громоздкими и сложными, но фактически обычному пользователю при расчете деревянных балок перекрытия важно просто представлять себе характер распределения действующих на балку сил и понимать – чтобы соблюсти условия прочности, необходимо правильно выбрать схему приложения нагрузок.

Упрощенный расчет балок перекрытия из дерева на прочность

В частном строительстве в основном используется схема 2.1 из таблицы 1.4, то есть равномерно распределенная по всей длине балки от стены до стены нагрузка. Ее величина определяется исходя из таблиц или экспериментально.

Поскольку балка работает не сама по себе, а в комплексе с другими, для расчета требуется информация о шаге расположения балок (на схеме Р).

Нагрузка на балки определяется типом перекрытия – чердачным или межэтажным. СНиП 2.01.07-85 дает такие данные (в кгс/м.кв. или в кПа, в скобках второе число):

• для чердачных перекрытий 130…245 (1,3…2,45);
• для мансарды 350 (3,5);
• для межэтажного перекрытия 400 (4).

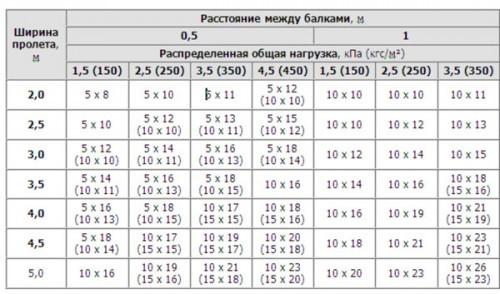
В соответствии с планируемыми длиной пролета, шагом балок (0,5 или 1 м) и ориентировочной нагрузкой выбирается сечение балки в сантиметрах по таблице 1.8.

Далее расчет ведется, исходя из условия прочности – максимальный изгибающий момент, деленный на момент сопротивления балки при изгибе, должен быть меньше предельно допустимого напряжения.

Для расчета момента используем формулы, приведенные в соответствующей таблице, для равномерно распределенной нагрузки на балку с защемлением в обоих концах это

Момент сопротивления при изгибе прямоугольной балки

Таким образом, расчет деревянной балки на прочность производим по формуле

Для примера возьмем пролет 3 м, балки в межэтажном перекрытии расположены с шагом 0,5 м, сечение (по таблице 1.8) 50х180 мм. Эти цифры дадут (с учетом перевода всех составляющих в единую размерность)

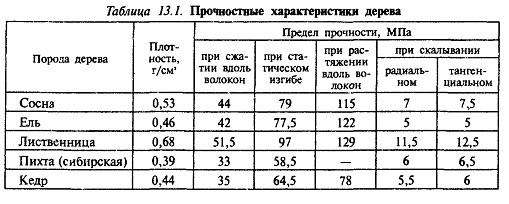
Что намного меньше предела прочности для сосны на изгиб (σ_max=79 МПа). Таким образом, расчетное значение сечения балки полностью удовлетворяет условию прочности и дает возможность нагрузить перекрытие даже больше, чем это предполагает СНиП.

Расчет перекрытия по деревянным балкам на допустимый изгиб

Из таблицы 1.4 видно, что максимальный допустимый изгиб балки должен составлять

Поскольку Е в этой формуле, как уже говорилось, это модуль упругости древесины, а I – это осевой момент инерции балки, необходимо найти модуль для конкретного вида древесины и рассчитать осевой момент по формуле c учетом того, что осевой эта величина измеряется в см⁴, то есть ширину балки b необходимо вставлять именно в сантиметрах.

Подставляя полученное значение в формулу расчета прогиба, получаем величину прогиба в метрах.

С учетом того, что для пролета 3 м максимально допустимый прогиб составляет одну трехсотую длины пролета, то есть 10 см, расчетное значение 3,9 см более чем удовлетворяет условиям задачи.

Заключение

Как видно из таблицы, выбранное значение сечения балки полностью обеспечивает выполнение условия прочности балки и дает прогиб значительно меньше допустимого. Таким образом, для черновых расчетов в частном строительстве можно спокойно пользоваться табличными данными, на всякий случай проверяя значения в онлайн-калькуляторе.